Measurement Tutorial
AC VOLTAGE AND CURRENT MEASUREMENT
4
4-13
measurements, for instance, cannot be made with dc coupling. Remember, however, that
when the 8842A measures signals with the ac functions, the reading on the display does
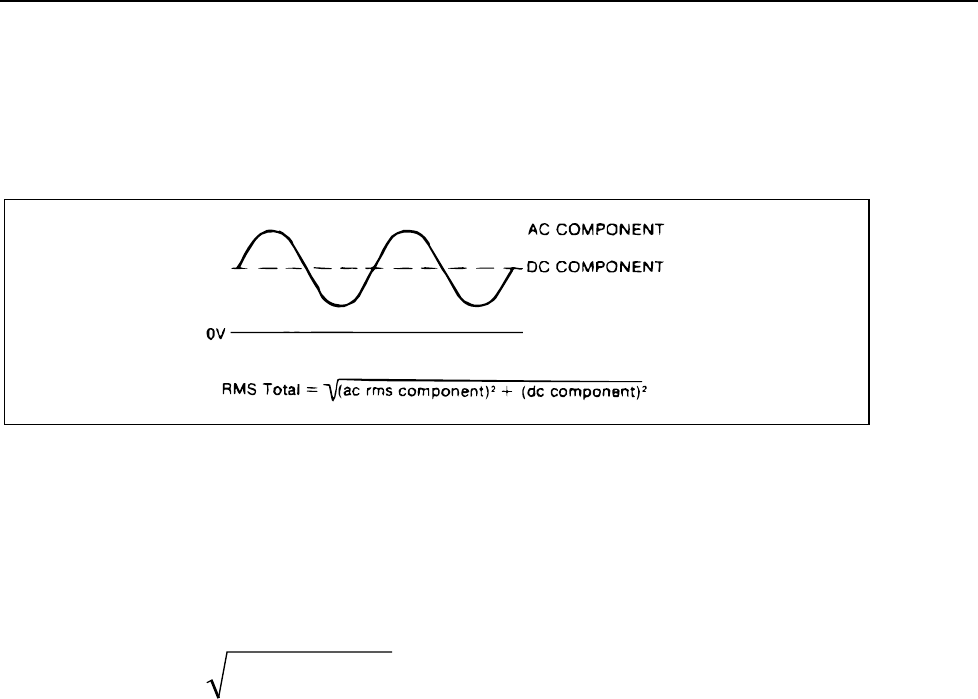
not include the dc component (if one exists). For example, consider Figure 4-8, which
shows a simple ac signal riding on a dc level. The VAC function would measure the ac
component only.
f4-08.wmf
Figure 4-8. Combined AC and DC Measurement
4-20. Combined AC and DC Measurements
The 8842A can be used to evaluate the true rms value of waveforms such as the one
shown in Figure 4-8, which includes both ac and dc components. First, measure the rms
value of the ac component using the VAC function. Next, measure the dc component
using the VDC function. Finally, calculate the total rms value as follows:
22
RMSV
DCAC
VV +=
4-21. Bandwidth
Bandwidth defines the range of frequencies to which an instrument can respond
accurately. The accuracy of the 8842A is specified for sinusoidal waveforms up to 100
kHz, or for nonsinusoidal waveforms with frequency components up to 100 kHz. The
small-signal bandwidth (the frequency at which the response is 3 dB down) is typically
around 300 kHz.
For signals with components greater than 100 kHz, the measurement accuracy is reduced
because of frequency bandwidth and slew-rate limitations. Because of this, accuracy may
be reduced when measuring signals with fast rise times, such as high-frequency square
waves or switching supply waveforms. As a rule of thumb, an ac voltage input signal is
within the bandwidth limitations if the rise time is longer than 2 us, and within the slew-
rate limitations if the input slew rate is slower than (1V/µs)x(full scale of range).
4-22. Zero-Input VAC Error
If the 8842A input terminals are shorted while the VAC function is selected, the 8842A
displays a non-zero reading (typically less than 80 digits in the highest four ranges, and
less than 300 digits in the 200 mV range). Such readings are due to random noise
combined with the inherent nonlinear response of computing-type rms converters to very
small input signals.


















